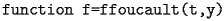Esercitazione su sistemi di equazioni differenziali ordinarie
Si vuole approssimare il moto di un pendolo di Foucault, moto descritto
dal seguente sistema di equazioni differenziali ordinarie:
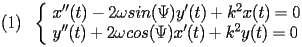
in cui
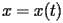 e
e
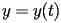 rappresentano
la posizione del pendolo (supposto di massa puntiforme) all'istante
temporale
rappresentano
la posizione del pendolo (supposto di massa puntiforme) all'istante
temporale
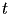 ,
,
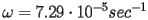 è la velocità della Terra,
è la velocità della Terra,
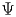 è
la latitudine a cui si trova il pendolo,
è
la latitudine a cui si trova il pendolo,
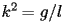 ,
,
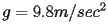 e
e
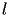 è la lunghezza
della corda del pendolo.
è la lunghezza
della corda del pendolo.
Si prendano
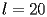 ,
,
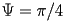 .
.
Al sistema si
possono aggiungere delle condizioni iniziali
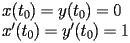
- Si riduca il sistema di equazioni differenziali del secondo ordine
ad un sistema di equazioni del primo ordine
- Si approssimi il sistema ottenuto con lo schema di Eulero Esplicito e
con lo schema predictor-corrector AB2-AM3 sull'intervallo
temporale
![$[0,300\ sec]$](lab8_files/lab8_13.gif) , scegliendo opportunamente il
parametro di discretizzazione
, scegliendo opportunamente il
parametro di discretizzazione
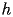 per entrambe i metodi.
per entrambe i metodi.
La scelta di
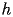 sia dettata da condizioni di stabilità e
di accuratezza.
sia dettata da condizioni di stabilità e
di accuratezza.
Poiché il moto del pendolo è periodico con ampiezza
costante, le coordinate
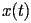 e
e
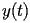 non si dovrebbero smorzare né amplificare
sensibilmente. In particolare lo smorzamento è dovuto alla
scarsa accuratezza (di fatto si ha una dissipazione artificiale
dovuta allo schema numerico), mentre l'amplificazione è dovuta
all'instabilità.
non si dovrebbero smorzare né amplificare
sensibilmente. In particolare lo smorzamento è dovuto alla
scarsa accuratezza (di fatto si ha una dissipazione artificiale
dovuta allo schema numerico), mentre l'amplificazione è dovuta
all'instabilità.
- Rappresentare graficamente la traiettoria del pendolo nel piano
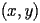 in funzione del tempo. A tale proposito si possono
utilizzare le istruzioni salvate nel file tempo.m.
in funzione del tempo. A tale proposito si possono
utilizzare le istruzioni salvate nel file tempo.m.
- Utilizzare la function di MATLAB ode45 (help ode45) per
risolvere lo stesso problema. A tale proposito bisogna definire una
nuova function in cui definire la funzione
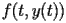 associata al sistema di equazioni differenziali.
associata al sistema di equazioni differenziali.
L'intestazione sarà
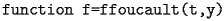
e dovrà costruire un vettore colonna f.
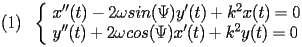
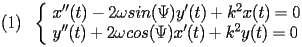
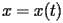 e
e
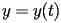 rappresentano
la posizione del pendolo (supposto di massa puntiforme) all'istante
temporale
rappresentano
la posizione del pendolo (supposto di massa puntiforme) all'istante
temporale
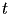 ,
,
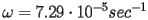 è la velocità della Terra,
è la velocità della Terra,
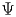 è
la latitudine a cui si trova il pendolo,
è
la latitudine a cui si trova il pendolo,
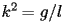 ,
,
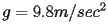 e
e
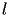 è la lunghezza
della corda del pendolo.
è la lunghezza
della corda del pendolo.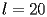 ,
,
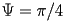 .
.
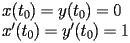
![$[0,300\ sec]$](lab8_files/lab8_13.gif) , scegliendo opportunamente il
parametro di discretizzazione
, scegliendo opportunamente il
parametro di discretizzazione
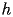 per entrambe i metodi.
per entrambe i metodi. 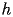 sia dettata da condizioni di stabilità e
di accuratezza.
sia dettata da condizioni di stabilità e
di accuratezza. 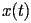 e
e
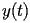 non si dovrebbero smorzare né amplificare
sensibilmente. In particolare lo smorzamento è dovuto alla
scarsa accuratezza (di fatto si ha una dissipazione artificiale
dovuta allo schema numerico), mentre l'amplificazione è dovuta
all'instabilità.
non si dovrebbero smorzare né amplificare
sensibilmente. In particolare lo smorzamento è dovuto alla
scarsa accuratezza (di fatto si ha una dissipazione artificiale
dovuta allo schema numerico), mentre l'amplificazione è dovuta
all'instabilità.
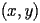 in funzione del tempo. A tale proposito si possono
utilizzare le istruzioni salvate nel file tempo.m.
in funzione del tempo. A tale proposito si possono
utilizzare le istruzioni salvate nel file tempo.m.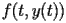 associata al sistema di equazioni differenziali.
associata al sistema di equazioni differenziali.