Esercitazione su equazioni differenziali ordinarie
Si consideri il seguente problema di Cauchy:
![\begin{eqnarray}\label{pdC}
\left\{\begin{array}{ll}
y'(t)=\lambda y(t)+g'(t)-\lambda g(t) & t\in (0,10]\\
y(t_0)=2,
\end{array}
\right.
\end{eqnarray}](lab7_files/lab7_1.gif)
dove
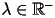 e
e
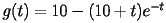 .
.
- Si approssimi il problema (1) con il metodo
predictor-corrector AB2-AM3, fissando
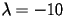 e si verifichi sperimentalmente che l'ordine di
accuratezza del metodo è 3, sapendo che la soluzione esatta del problema
dato è
e si verifichi sperimentalmente che l'ordine di
accuratezza del metodo è 3, sapendo che la soluzione esatta del problema
dato è
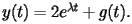
-
Per
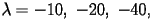 plottando la soluzione
numerica ed osservandone il comportamento convergente o divergente
per
plottando la soluzione
numerica ed osservandone il comportamento convergente o divergente
per
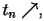 si determini sperimentalmente la limitazione su
si determini sperimentalmente la limitazione su
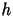 affinché
si abbia assoluta stabilità
(si considerino 2 cifre decimali per la mantissa di
affinché
si abbia assoluta stabilità
(si considerino 2 cifre decimali per la mantissa di
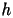 ).
).
In base ai risultati ottenuti, determinare una costante
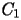 ,
indipendente da
,
indipendente da
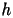 e
e
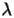 , tale che la regione di assoluta
stabilità dello schema AB2-AM3,
ristretta all'asse reale, si possa esprimere
come
, tale che la regione di assoluta
stabilità dello schema AB2-AM3,
ristretta all'asse reale, si possa esprimere
come
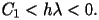
- Si consideri
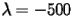 .
In base al valore di
.
In base al valore di
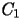 determinato ai punti precedenti, si diano limitazioni su
determinato ai punti precedenti, si diano limitazioni su
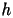 per avere assoluta stabilità.
Utilizzare sempre 2 cifre decimali per la mantissa di
per avere assoluta stabilità.
Utilizzare sempre 2 cifre decimali per la mantissa di
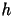 .
Verificare sperimentalmente la validità della
limitazione ottenuta.
.
Verificare sperimentalmente la validità della
limitazione ottenuta.
- Determinare il massimo valore di
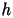 per cui l'errore sulla
soluzione esatta in
per cui l'errore sulla
soluzione esatta in
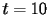 sia minore o uguale a
sia minore o uguale a
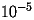 . (si considerino sempre due cifre decimali per
la mantissa di
. (si considerino sempre due cifre decimali per
la mantissa di
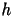 ).
).
In base a quanto trovato il problema si può classificare come problema
stiff? Giustificare la risposta.
![\begin{eqnarray}\label{pdC}
\left\{\begin{array}{ll}
y'(t)=\lambda y(t)+g'(t)-\lambda g(t) & t\in (0,10]\\
y(t_0)=2,
\end{array}
\right.
\end{eqnarray}](lab7_files/lab7_1.gif)
![\begin{eqnarray}\label{pdC}
\left\{\begin{array}{ll}
y'(t)=\lambda y(t)+g'(t)-\lambda g(t) & t\in (0,10]\\
y(t_0)=2,
\end{array}
\right.
\end{eqnarray}](lab7_files/lab7_1.gif)
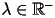 e
e
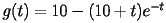 .
.
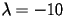 e si verifichi sperimentalmente che l'ordine di
accuratezza del metodo è 3, sapendo che la soluzione esatta del problema
dato è
e si verifichi sperimentalmente che l'ordine di
accuratezza del metodo è 3, sapendo che la soluzione esatta del problema
dato è
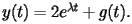
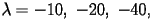 plottando la soluzione
numerica ed osservandone il comportamento convergente o divergente
per
plottando la soluzione
numerica ed osservandone il comportamento convergente o divergente
per
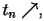 si determini sperimentalmente la limitazione su
si determini sperimentalmente la limitazione su
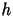 affinché
si abbia assoluta stabilità
(si considerino 2 cifre decimali per la mantissa di
affinché
si abbia assoluta stabilità
(si considerino 2 cifre decimali per la mantissa di
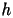 ).
). 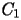 ,
indipendente da
,
indipendente da
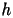 e
e
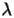 , tale che la regione di assoluta
stabilità dello schema AB2-AM3,
ristretta all'asse reale, si possa esprimere
come
, tale che la regione di assoluta
stabilità dello schema AB2-AM3,
ristretta all'asse reale, si possa esprimere
come
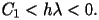
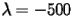 .
In base al valore di
.
In base al valore di
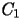 determinato ai punti precedenti, si diano limitazioni su
determinato ai punti precedenti, si diano limitazioni su
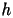 per avere assoluta stabilità.
Utilizzare sempre 2 cifre decimali per la mantissa di
per avere assoluta stabilità.
Utilizzare sempre 2 cifre decimali per la mantissa di
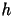 .
Verificare sperimentalmente la validità della
limitazione ottenuta.
.
Verificare sperimentalmente la validità della
limitazione ottenuta.
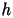 per cui l'errore sulla
soluzione esatta in
per cui l'errore sulla
soluzione esatta in
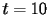 sia minore o uguale a
sia minore o uguale a
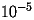 . (si considerino sempre due cifre decimali per
la mantissa di
. (si considerino sempre due cifre decimali per
la mantissa di
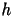 ).
).