Generazione di una mesh strutturata su un cerchio
Si vuole rappresentare graficamente una funzione
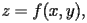 sul cerchio di
sul cerchio di
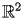 di centro l'origine e raggio 1.
di centro l'origine e raggio 1.
A tale proposito si vuole generare una mesh strutturata (ovvero una
opportuna trasformazione di una griglia
cartesiana), in modo
da poter utilizzare le function di MATLAB mesh, surf, meshc,....
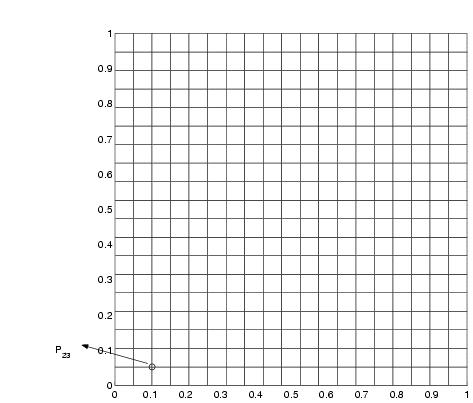
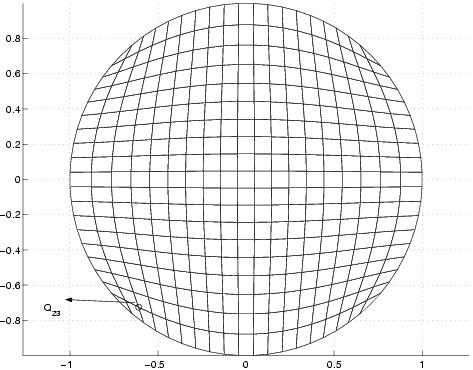 In alto la mesh cartesiana sul quadrato
In alto la mesh cartesiana sul quadrato
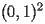 (20 x 20 punti),
in basso la trasformazione della mesh cartesiana sul cerchio (sempre
20 x 20 punti).
(20 x 20 punti),
in basso la trasformazione della mesh cartesiana sul cerchio (sempre
20 x 20 punti).
Ogni punto
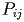 (con
(con
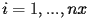 e
e
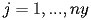 ) del quadrato viene trasformato nel
corrispondente
) del quadrato viene trasformato nel
corrispondente
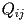 del cerchio (sempre con
del cerchio (sempre con
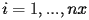 e
e
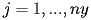 ).
).
Per generare tale griglia si devono risolvere due sistemi lineari
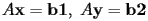 ,
in cui i vettori incogniti
,
in cui i vettori incogniti
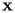 e
e
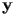 contengono le coordinate
(rispettivamente ascisse e ordinate) dei punti della griglia.
contengono le coordinate
(rispettivamente ascisse e ordinate) dei punti della griglia.
Indicando con
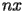 e
e
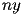 il numero di punti
lungo la direzione
il numero di punti
lungo la direzione
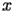 e
e
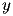 , rispettivamente,
i sistemi lineari da risolvere hanno dimensione
, rispettivamente,
i sistemi lineari da risolvere hanno dimensione
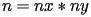 .
Il vettore x, soluzione di A x=b1, contiene le
ascisse dei punti del cerchio, ordinati (rispetto ai punti corrispondenti
del quadrato) da sinistra a destra e dal basso verso l'alto,
ovvero x(1) contiene l'ascissa del punto
.
Il vettore x, soluzione di A x=b1, contiene le
ascisse dei punti del cerchio, ordinati (rispetto ai punti corrispondenti
del quadrato) da sinistra a destra e dal basso verso l'alto,
ovvero x(1) contiene l'ascissa del punto
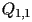 ,
x(nx) contiene l'ascissa del punto
,
x(nx) contiene l'ascissa del punto
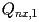 ,
x(nx+1) contiene l'ascissa del punto
,
x(nx+1) contiene l'ascissa del punto
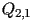 ,
ecc.,
x(n) contiene l'ascissa del punto
,
ecc.,
x(n) contiene l'ascissa del punto
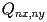 .
Analogo discorso vale per il vettore y contenente le ordinate
dei punti
.
Analogo discorso vale per il vettore y contenente le ordinate
dei punti
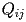 .
Fissati
.
Fissati
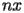 e
e
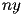 , la matrice
A ed i termini noti b1 e
b2 sono generati mediante la chiamata alla
function griglia.m:
, la matrice
A ed i termini noti b1 e
b2 sono generati mediante la chiamata alla
function griglia.m:
[A,b1,b2]=griglia(nx,ny).
Si chiede di:
- Analizzare le proprietà della matrice A
(dominanza diagonale stretta, simmetria, definita positività) e dire
a priori quali metodi iterativi possono essere utilizzati per la
risoluzione dei sistemi A x=b1 e A y=b2.
- Risolvere i sistemi lineari A x=b1 e A y=b2
con il metodo di Jacobi ( help jacobi), prendendo toll=1.e-6,
kmax = 500, x0=rand(n,1).
Rappresentare su un grafico la storia di
convergenza del metodo, ovvero il vettore err, contenente
le quantità
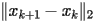 , per
, per
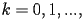 fino a convergenza o fino a kmax.
fino a convergenza o fino a kmax.
Nel caso in cui in kmax iterazioni non si abbia convergenza,
si può portare a convergenza il metodo?
- Risolvere i sistemi lineari A x=b1 e A y=b2
con il metodo di Gauss-Seidel ( help gaussseidel),
prendendo toll=1.e-6, kmax = 500, x0=rand(n,1).
Rappresentare su un grafico la storia di
convergenza del metodo, ovvero il vettore err, contenente
le quantità
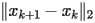 , per
, per
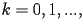 fino a convergenza o fino a kmax.
fino a convergenza o fino a kmax.
Nel caso in cui in kmax iterazioni non si abbia convergenza,
si può portare a convergenza il metodo?
- Stimare il raggio spettrale delle matrici di iterazione di Jacobi e
Gauss-Seidel.
I valori ottenuti confermano quanto trovato ai
punti percedenti?
- Risolvere i sistemi lineari A x=b1 e A y=b2
con il metodo bicgstab ( help bicgstab) con
toll=1.e-6, kmax = 500, x0=rand(n,1). Richiamare la
function con 5 parametri di output e 7 parametri di input, ponendo
il quinto ed il sesto uguali a [].
Rappresentare su un grafico la storia di
convergenza del metodo, ovvero il vettore resvec, contenente
le quantità
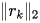 , per
, per
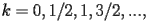 fino a convergenza. Plottare
le componenti di resvec con
fino a convergenza. Plottare
le componenti di resvec con
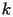 intero.
intero.
- Confrontare le storie di convergenza dei tre metodi e commentare
i risultati ottenuti.
- Rappresentare graficamente la mesh e la funzione
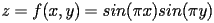 .
.
A tale scopo bisogna riordinare i vettori
x e y in forma di matrici di ny righe e
nx colonne, seguendo l'ordinamento indicato sopra.
Scrivere una function (converti.m) che,
dato in input un vettore x di
dimension n=nx*ny, dia la matrice xh di
ny righe e nx colonne.
Utilizzare il comando mesh per visualizzare la mesh,
ed utilizzare il comando meshc per visualizzare la funzione
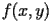 .
.


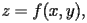 sul cerchio di
sul cerchio di
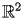 di centro l'origine e raggio 1.
di centro l'origine e raggio 1.

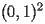 (20 x 20 punti),
in basso la trasformazione della mesh cartesiana sul cerchio (sempre
20 x 20 punti).
(20 x 20 punti),
in basso la trasformazione della mesh cartesiana sul cerchio (sempre
20 x 20 punti).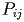 (con
(con
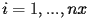 e
e
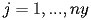 ) del quadrato viene trasformato nel
corrispondente
) del quadrato viene trasformato nel
corrispondente
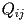 del cerchio (sempre con
del cerchio (sempre con
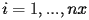 e
e
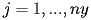 ).
).
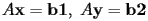 ,
in cui i vettori incogniti
,
in cui i vettori incogniti
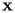 e
e
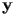 contengono le coordinate
(rispettivamente ascisse e ordinate) dei punti della griglia.
contengono le coordinate
(rispettivamente ascisse e ordinate) dei punti della griglia.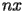 e
e
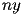 il numero di punti
lungo la direzione
il numero di punti
lungo la direzione
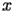 e
e
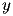 , rispettivamente,
i sistemi lineari da risolvere hanno dimensione
, rispettivamente,
i sistemi lineari da risolvere hanno dimensione
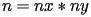 .
Il vettore x, soluzione di A x=b1, contiene le
ascisse dei punti del cerchio, ordinati (rispetto ai punti corrispondenti
del quadrato) da sinistra a destra e dal basso verso l'alto,
ovvero x(1) contiene l'ascissa del punto
.
Il vettore x, soluzione di A x=b1, contiene le
ascisse dei punti del cerchio, ordinati (rispetto ai punti corrispondenti
del quadrato) da sinistra a destra e dal basso verso l'alto,
ovvero x(1) contiene l'ascissa del punto
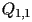 ,
x(nx) contiene l'ascissa del punto
,
x(nx) contiene l'ascissa del punto
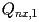 ,
x(nx+1) contiene l'ascissa del punto
,
x(nx+1) contiene l'ascissa del punto
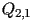 ,
ecc.,
x(n) contiene l'ascissa del punto
,
ecc.,
x(n) contiene l'ascissa del punto
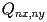 .
Analogo discorso vale per il vettore y contenente le ordinate
dei punti
.
Analogo discorso vale per il vettore y contenente le ordinate
dei punti
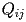 .
Fissati
.
Fissati
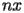 e
e
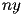 , la matrice
A ed i termini noti b1 e
b2 sono generati mediante la chiamata alla
function griglia.m:
, la matrice
A ed i termini noti b1 e
b2 sono generati mediante la chiamata alla
function griglia.m: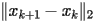 , per
, per
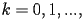 fino a convergenza o fino a kmax.
fino a convergenza o fino a kmax.
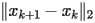 , per
, per
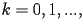 fino a convergenza o fino a kmax.
fino a convergenza o fino a kmax.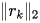 , per
, per
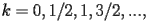 fino a convergenza. Plottare
le componenti di resvec con
fino a convergenza. Plottare
le componenti di resvec con
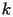 intero.
intero.
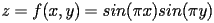 .
. 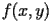 .
.